

These points are referred to as 𝐽 double prime, 𝐾 double prime, and 𝐿 double prime as they’re the images of 𝐽, 𝐾, and 𝐿 after two reflections. So we’re going to keep the new 𝑦-coordinates the same, but multiply the 𝑥-coordinates by negative one. And remember the effect here is on the 𝑥-coordinates. The second reflection is over the 𝑦-axis. So in the image of the three points 𝐽, 𝐾, and 𝐿, which is 𝐽 prime, 𝐾 prime, and 𝐿 prime, the 𝑥-coordinates are the same, but the 𝑦-coordinates have been multiplied by negative one. The first reflection in the 𝑥-axis multiplies the 𝑦-coordinates by negative one. So we begin with the coordinates of the three points 𝐽, 𝐾, and 𝐿. Let’s actually perform this reflection on the vertices 𝐽, 𝐾, and 𝐿. So now we’ve seen what will happen to the 𝑥- and 𝑦-coordinates after each reflection.
Again, this effect on the 𝑥- and 𝑦-coordinates is a general rule that you should memorize. Therefore, this time, it’s the 𝑥-coordinate that is multiplied by negative one. Points swap from the left to the right of the 𝑦-axis and vice versa, which means the 𝑥-values change from positive to negative or negative to positive. Again, for the general point with coordinates 𝑥, 𝑦, the 𝑦-axis is a vertical line, which means the effect of this reflection is horizontal. Now, let’s think about what happens when you reflect over the 𝑦-axis. And so this is achieved by multiplying the 𝑦-coordinate by negative one. Positive values become negative and negative values become positive. Points above the mirror line now appear below the mirror line and points below now appear above, which means it’s the 𝑦-coordinate that is being affected. The 𝑥-axis is a horizontal line, which means the effect of the reflection is vertical. This is a general rule, which you should memorize.īut to see where it comes from, just picture the effect of reflecting in the 𝑥-axis. So the point 𝑥, 𝑦 gets mapped to the point with coordinates 𝑥, negative 𝑦. Well, the effect is the 𝑦-coordinate is multiplied by negative one.

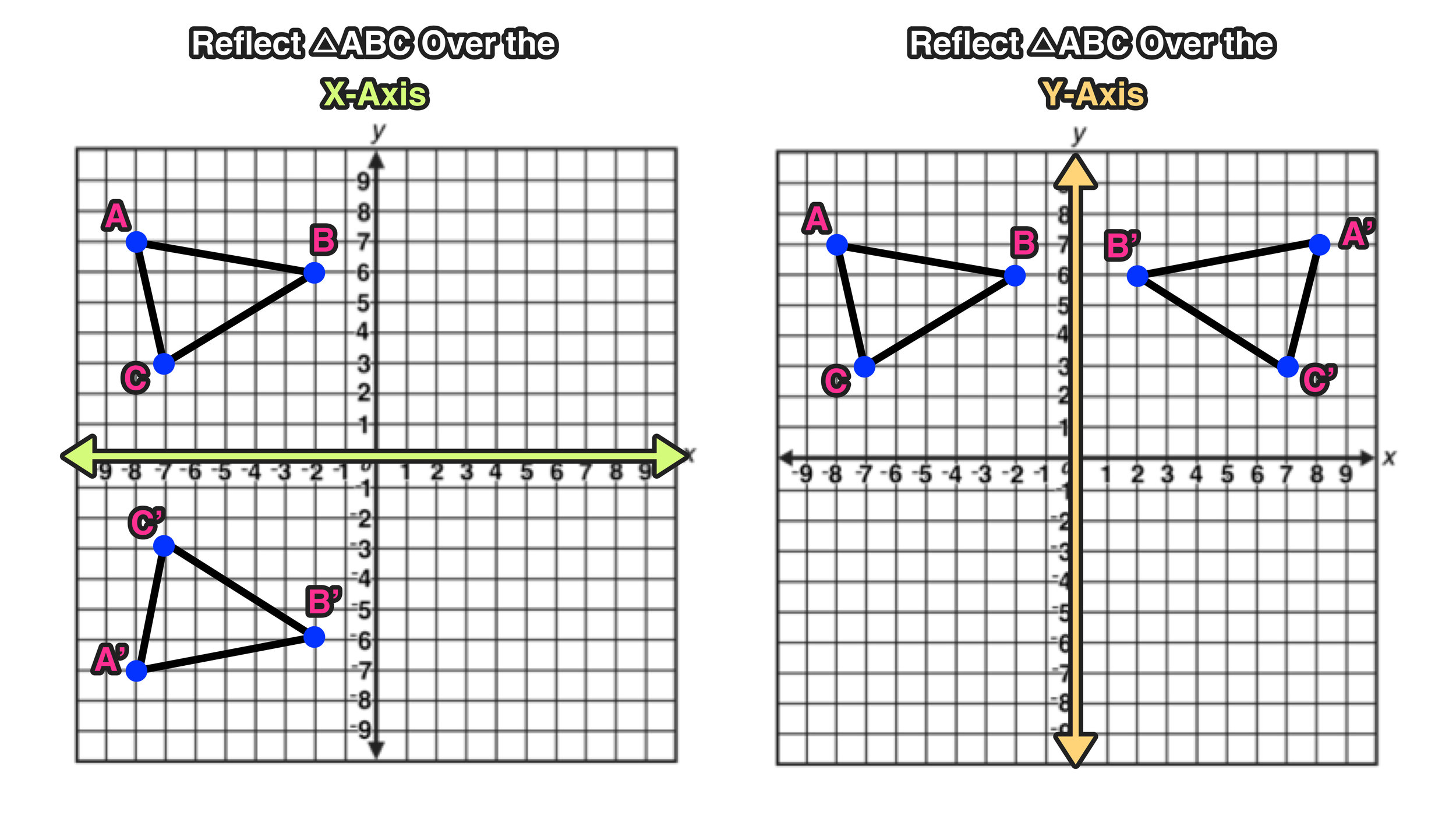
So let’s think about what happens to the general point with coordinates 𝑥, 𝑦 when it’s reflected over the 𝑥-axis.

We need to find another method of answering this question. And we’re asked to do this without graphing, which means we’re not supposed to plot these points on a coordinate grid and then use this to help in our answer. We are asked to find the coordinates of the images of these three points. These three points are undergoing two reflections: firstly, over the 𝑥-axis and secondly, over the 𝑦-axis. So we’re given the coordinates of three points: 𝐽, 𝐾, and 𝐿. The reflecting line is the perpendicular bisector of all segments that connect pre-image locations to their corresponding image points when a figure is reflected.Given that vertices 𝐽 negative eight, eight, 𝐾 three, negative nine, and 𝐿 negative three, five form a triangle, without graphing determine their coordinates after a reflection over the 𝑥-axis first and then over the 𝑦-axis. The point \(\left( \right).\)Īns: A perpendicular bisector is a reflecting line. \(MR \bot AA’.\) The mirror line is perpendicular bisector to the line joining the point and its image. \(OA=OA’.\) The distance of a point from the mirror is the same as the distance of its image.Ģ. If you look at the image of a point \(A\) in the mirror \(MR,\) as shown in the figure, you will find it at \(A’.\) Let \(AA’\) intersect \(MR\) at \(O.\) We find thatġ. Reflection symmetry is a concept utilised in the design of astronomical telescopes. Note: Any object’s reflected image is identical to the object itself. The line of reflection refers to a single line that aids in the reflection of an object. Both figures (before and after reflection) are equidistant from all places on their respective surfaces.ĥ. Because the position has altered because of the transformation, there are possibilities for translation as well.Ĥ. The size and shape, however, remain the same.ģ. The only difference is that the generated image is in the opposite direction. As a result, the final image will reflect the original structure.Ģ. In geometry, flipping an image is known as a reflection.


 0 kommentar(er)
0 kommentar(er)
